О приближенном решении дифференциальных уравнений, общее решение которых зависит. Дифференциальное уравнение, (2.13) Где,, – известные функции, называется Уравнением Риккати.

• Уравнение Риккати Реферат
• Уравнение Риккати Курсовая

ИССЛЕДОВАНИЕ МАТРИЧНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РИККАТИ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ Копец Мирослав Михайлович канд. Наук, доцент НТУУ «КПИ», г. Киев Е-mail: 1. Введение Диффенциальное уравнение Риккати — это диффенциальное уравнение первого порядка, правая часть которого представляет собой квадратный трехчлен относительно неизвестной функции. Таким названием это уравнение обязано статье итальянского математика Якопо Франческо Риккати, опубликованной в 1724 году 14. Несмотря на прошедшие почти три столетия, интерес к уравнению Риккати нисколько не ослабевает. В первую очередь к уравнениям Риккати приводят задачи оптимального управления, задачи теории дифференциальных игр, задачи построения оптимальных фильтров Калмана — Бьюси, двухточечные краевые задачи с использованием метода прогонки. Также уравнения Риккати появляются при решении задач динамики процессов в сплошных средах, задач теории теплопроводности и диффузии, задачи нахождения решений матричных телеграфных уравнений.

В основном, в перечисленных выше случаях, как правило, приходится исследовать матричные диффенциальные урав­нения Риккати, в которых неизвестная зависит только от одной перемен­ной. Такая ситуация возникает тогда, когда рассматриваются системы со сосредоточенными параметрами. Именно для таких случаев основные свойства матричных диффенциальных уравнений Риккати изучены наиболее полно 1—6, 10—13. Для математических моделей систем с распределенными параметрами возникают матричные диффен­циальные уравнения Риккати с частными производными 7, 9, 12,матричные интегродиффенциальные уравнения Риккати, которые менее исследованы по сравнению с обычными матричными диффенциаль­ными уравнениями Риккати. Постановка задачи Рассматривается следующая система уравнений (1) где, — заданные матрицы размера, — заданная матрица размера, — заданная симметричная положительно определенная матрица размера ( поэтому существует матрица ), причем все эти пять матриц — постоянные (их элементами являются действительные числа), — симметричная неотрицательно определенная матрица размера, символы, и соответственно обозначают транспонированные матрицы,. Заданы действительные числа и такие, что,.

Искомая матричнозначная функция при каждой упорядоченной паре фиксированных значений и имеет размер и удовлетворяет условию, (2) где: — симметричная неотрицательно определенная матрица размера. Задача (1)—(2) обязана своим возникновением следующей задаче оптимизации: найти управление, на котором реализуется минимум функционала при условии, что состояние управляемой системы является решением системы уравнений з частными производными, удовлетворяет начальному условию и краевым условиям, где — мерные векторнозначные функции, заданы, — мерная векторнозначная функция должна быть найдена. По аналогии с конечномерным случаем первое уравнение системы (1) естественно назвать матричным дифференциальным уравнением Риккати с частными производными 7. Основные свойства матричного дифференциального уравнения Риккати с частными производными Рассмотрим следующее матричное уравнение (3) с дополнительными условиями (4). (5) Предположим, что задача (3)—(5) имеет единственное решение.

Если в уравнении (3) выполнить операцию транспонирования, то получим (6) Из условия (4) имеем. Поэтому и, следовательно,. (7) Кроме того, в силу симметричности матрицы имеем. (8) Подставляя (7) в (6) и принимая во внимание равенство (8), видим, что и являются решениями одной и той же задачи (3) — (5). В силу единственности решения этой задачи приходим к выводу,.

Таким образом, доказано следующее утверждение. Если задача (3)—(5) имеет единственное решение, то тогда справедливо равенство, то — есть для каждой упорядоченной фиксированной пары где решение является симметрической матрицей порядка. Теорема 2. Решение задачи (3) — (5) можно представить в следующем виде, (9) где: функции и удовлетворяют системе уравнений (10) и дополнительному условию (11) при условии, что матричнозначная функция существует. Доказательство. Ищем решение уравнения (3) в виде произведения, (12) где: и — пока неизвестные функции. Непосредственно из соотношения (12) имеем (13).

(14) Подставляя (12), (13) и (14) в уравнение (3), получим. (15) Теперь предположим, что существует матричнозначная функция. После умножения справа уравнения (7) на матрицу имеем.

(16) Уравнение (16) можно преобразовать следующим образом, (17) поскольку имеет место равенство, и, поэтому, справедливо также и равенство. Очевидно, что уравнение (9) переписать так. (18) Равенство (18) будет иметь место, если одновременно выполняются следующие два равенства (19). (20) Дальше в уравнениях (19) и (20) сделаем замену. Поскольку справедливы следующие равенства и, то с учетом этих замечаний совокупность уравнений (19) и (20) можно переписать в виде системы уравнений. (21) Наконец, из равенств и получаем, что и требовалось доказать.

Теорема 3. Если рассмотреть блочную матрицу размера, (22) то систему уравнений (21) можно записать в следующем виде, (23) где — квадратная матрица размера, все элементы которой равны нулю. Доказательство. Действительно, путем непосредственного вычисления находим Подобным образом устанавливается и следующее утверждение. С помощью матрицы (15) систему (1) можно записать в блочной форме, (24) где — единичная матрица размера, — квадратная матрица размера, все элементы которой равны нулю.

В самом деле, имеем Дальше находим. Таким образом, окончательно получим,. Это означает, что равенство (24) доказано. Теорема 5. Пусть функция есть частным решением уравнения (3) Если — некоторое другое решение уравнения (3), отличное от, то функция удовлетворяет следующему матричному уравнению Бернулли с частными производными, (25) где:,. При этом выполняется равенство.

Из равенства непосредственно имеем. Подставляя эти выражения в уравнение (3), получим. (26) Поскольку, то уравнение (26) перепишется так. Введем обозначение. В результате окончательно имеем. Кроме того, из равенств и следует также,.

Это означает, что теорема 5 доказана. С помощью замены уравнение (25) сводится к линейному уравнению. Подставляя эти выражения в уравнение (25), получим. (27) Поскольку, то это означает,. Следовательно, равенство (27) будет иметь вид.

Умножая последнее равенство слева на матрицу, получим. После умножения этого уравнения справа на матрицу окончательно имеем. (28) Таким образом, уравнение (28) является линейным относительно неизвестной функции. При этом выполняется равенство. Пусть известно частное решение уравнения (28). Тогда это уравнение можно свести к однородному уравнению, если выполнить замену. Соответствующее однородное уравнение имеет вид.

(29) Очевидно, что дополнительно имеет место равенство. Решение уравнения (29) ищем в виде следующего произведения, где — произвольная постоянная матрицы размера, и — неизвестные матрицы такого же размера. Отсюда следует, что И.

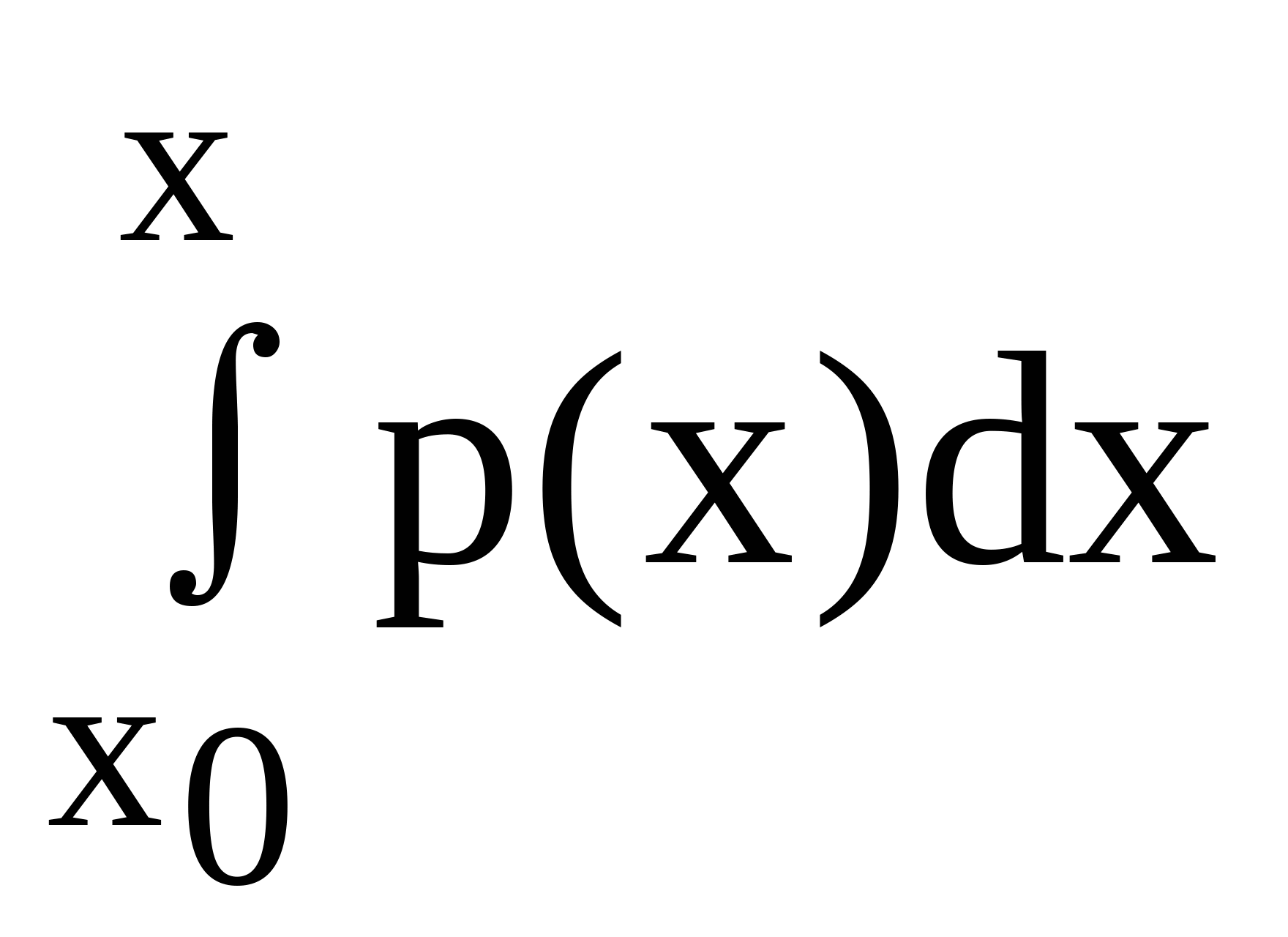
Подставляя эти выражения в уравнение (29), в результате имеем. Перепишем это уравнение следующим образом. (30) Поскольку, то, и, то уравнение (30) примет вид.

Это равенство выполняется, если одновременно выполняются следующие два равенства (31) Умножая второе уравнение системы (31) сперва на матрицу слева, потом на эту же матрицу справа, получим. (32) Дальше сделаем замену. Поскольку и, то уравнение (32) примет вид.

Microsoft project portable. Таким образом, система (31) примет вид (33) Уравнение (3) можно записать в симметрической форме. Действительно, из условия следует,. Поэтому уравнение (3) можно переписать так (34) Уравнение (34) естественным образом порождает следующую блочную матрицу (35) размера. Теорема 7. С помощью матрицы (35) уравнение (34) можно представить таким образом. С помощью непосредственного вычисления находим, что и требовалось доказать. Список литературы:.

Андреев Ю. А. Управление конечномерными линейными объектами. — М.: Наука, 1976. Бублик Б. Н., Кириченко Н. Ф. Основы теории управления. — Киев, издательское объединение «Вища школа», 1975.

Уравнение Риккати Реферат

Егоров А. И. Уравнение Риккати.

— М.: ФИЗМАТЛИТ, 2001. Захар — Иткин М. Х.

Методы численного решения граничных задач для матричных телеграфных уравнений. // Электричество — 1971. — Том 2 — с. 33—37. Захар — Иткин М. Х.

Матричное дифференциальное уравнение Риккати и полугруппа дробно — линейных преобразований. — Том XXVIII, вып.3 (171) — с. 83—120.

Зеликин М. И. Однородные пространства и уравнение Риккати в вариационном исчислении. — М.: Изд — во «Факториал», 1998. Копец М. М. Оптимальное управление объектом, описываемым сингулярной системой линейных уравнений с частными производными. // «Математика и информационные технологии в современном мире», материалы международной заочной научно — практической конференции.

Уравнение Риккати Курсовая

— Новосибирск, 2011. Лионс Ж.—Л. Оптимальное управление системами, описываемыми уравнениями с частными производными. — М.: Мир, 1972. Лурье К. А.

Оптимальное управление в задачах математической физики. М.: Наука, 1975. Ройтенберг Я. Н. Автоматическое управление. — М.: Наука, 1978. Bittanti S., Laub A. J., Willems J. C. The Riccati equation.

New York: Springer — Verlag, 1991. Curtain R. F., Pritchard A. J.

Functional analysis in modern applied mathematics. — Academic press: London — New York — San Francisco. Lancaster P., Rodman L. Algebraic Riccati equation. — Oxford University Press.

Animadversationes in aequationes differentiales secondi gradus. // Actorum eruditorum quae Lipsiare publicantur. — Supplementa 8, — p. 66—73.